以下是中七同學 Justin 早前的留言。
John sir早前上堂提到 complex number: i 和 0 大小比較的問題
當時的內容:
設, then
,則
, contradiction。反之設
, 亦生矛盾。
">"關係能滿足以下四個性質:
1)對任何兩個不同的數;
or
不能同時成立
2)if,
then
3)ifthen
4)if,
then
現設
by 4),
書中提到此未能導致矛盾(*)
(因為”>”不一定是實數中規定的含義)←這和阿sir上堂提到的問題有分別。
繼續:
利用剛得到的,by 4), both sides time
then
,
(這裏並未有將inequality sign倒轉),這裡是否和(*)所提到的有關?
we have
by property 3), add 1 into both sides
,then
by from above,and
,which contradicts property 1)
then we can conclude thatis not
反之也有同樣結果
然而,我的問題是:inequality sign 的使用層面 or 定義有沒有特定規限?因為 (*)
感謝同學指出我的錯誤。我以『-1 > 0』證明『複數不能比較大小』是太快得到結論。讓我趁機又吹吹水。
小孩初接觸自然數,
1,2,3,…
自然地為數字『排序』, 1 先,之後是 2,之後是 3,如此類推。及後,我們引入『不等式』符號 <,得到
1 < 2 < 3 < …
代表著一種『序』(order),也方便我們把兩個自然數比較大小,諸如 3 比 5 小,記之曰 3 < 5。
數學上,我們有辦法定義其他不同的『序』,比如,我們真的可以有
1 > 2,2 > 3 等等(參考 order dual)
那個符號『>』,就不是我們一般的大於(not in usual sense),而是符合某些條件的一種『序』。
對於 complex numbers,我們可否定義出一種『序』?
可以,最常用的是『字典排序』(lexicographic order),即是把字編入字典的方法,比如编 happy 先於 harass,因為我們由左至右比較字母,頭兩個也一樣,直至發覺 p 先於 r,便規定 happy 先於 harass。不妨記之曰 happy < harass。
對 complex number,我們不妨定
a + bi < c + di 當且僅當 a < c 或 (a = c 及 b < d)
(當心,在 A-level 千萬不可出現 a + bi < c + di 等等的式子,老師會二話不說給你零蛋。我們現在討論的是一種『序』,隨便你用什麼符號,但用『<』,是讓我們有一種熟悉的感覺而已,它不一定是一般的不等式符號,它只用來表達熟先熟後的標記。所以 Justin 可以放心,在中學,『<』這個符號一定是代表『嚴格小於』,只是到了大學,就要看情況了。)
由上述定義,我們有
3 + 100i < 4 + 2i
5 + 6i < 5 + 7i
8 – 2i < 8
等等。
(大家領略到好像『查字典』的感覺嗎?)
那麼,任何兩個 complex numbers,我也可以『知其先後』。
但,我們一般不會稱:任何兩個 complex numbers 都可『比較大小』。
其實,何謂『序』?數學上,『序』是一種關係(relation),起碼包括以下三種:
1. 偏序(partial order):亦可再細分為弱偏序及嚴格偏序
2. 線序(linear order)或稱全序(total order)
3. 良序(well order)
先談偏序。
設 A 是一個集。如果存在一種關係,姑且稱之曰 ,滿足以下 3 個特性
(自身性 reflexivity)對所有 a A, 恒有 a
a。
(反對稱性 antisymmetry)對所有 a , b A, 若 a
b 及 b
a,則 a = b。
(傳遞性 transitivity)對所有 a , b , c A, 若 a
b 及 b
c,則 a
c。
我們稱滿足上述 3 個條件的關係 為偏序。存在這種偏序的集,稱為偏序集(partially ordered set,或稱 poset)。只要考慮一般意義下的不等式
,整數集明顯地是偏序集。
讓我給一個非不等式的例子。
例如
命
a = {1}
b = {2}
c = {3}
d = {1,2}
e = {1,3}
f = {2,3}
g = {1,2,3}
設 A = {a,b,c,d,e,f,g}
我們很容易為 A 定義一種偏序,就是所謂 set inclusion。即
x y iff x
y
見上例,因 a d,有 a
d。又例如,b
d 而 d
g,有 b
g;亦表示 b
d,d
g,有 b
g。
因為 存在自身性,反對稱性和傳遞性,立知
亦符合這 3 個條件,即
是偏序。
Justin 給的序和偏序差不多,即是所謂嚴格偏序(strict order)。
設 A 是一個集。如果存在一種關係,姑且稱之曰 ,滿足以下 3 個特性
(非自身性 irreflexivity)對所有 a A, 無 a
a。
(非對稱性 asymmetry)對所有 a , b A, 若 a
b,則無 b
a。
(傳遞性 transitivity)對所有 a , b , c A, 若 a
b 及 b
c,則 a
c。
稍微推論一下,我們可以由『傳遞性』及『非自身性』推出『非對稱性』,那麼嚴格偏序的條件可減少到 2 個。
相對於嚴格偏序,有人稱前一種偏序為弱偏序。
單有偏序,足夠嗎?不,起碼,偏序不能滿足我們習以為常的一種認為:任何兩個數都可以『比較』。
舉例,我們在正整數集上定義這樣的一種偏序:若 a 整除 b,則定義 a b。例如
2 6 [因 2 整除 6]
5 20 [因 5 整除 20]
只要稍微檢查,可知這種序滿足偏序的三個要求:自身性,反對稱性和傳遞性。然而,對於某對正整數,諸如 4 和 5,因 4 不整除5 及 5 也不整除 4,故我們既無 4 5 亦無 5
4。這就是所謂不能『比較』了。
那麼,我們只要在嚴格偏序條件上加多一個:所謂『三分律』或『三一律』,即集合中任何兩個元素必有『三種關係』的其中一種,即
(三分律 trichotomy)對所有 a , b A, 必有 a
b, b
a 或 a = b。
滿足非自身性,非對稱性,傳遞性再加上三分律這四個條件的偏序,稱為線序或全序。
『線』者,取其把所有『元素』都可如『數線』,按序排列。
『全』者,即謂『全部』元素都可知其先後。
稍微檢查一下,複數集上定義的『字典排序』:a + bi < c + di 當且僅當 a < c 或 (a = c 及 b < d)
是全序,故複數集是所謂全序集。
如果複數集只是盛載著複數的集合,沒有任何運算發生的話,這個數學物體可說是沒有價值。但當我們在這個集合賦予了一些運算,諸如加減乘除,我們彷彿把這個死物『有機化』,滿注『生命力』。當複數集定義了『加法』和『乘法』後,這個東西不單是複數集,數學上,我們可稱它為複數域(field)。
如果有個域 F(簡單說,就是可以在 F 當中定義『加法』和『乘法』兩種運算),一旦存在全序 滿足額外的兩個要求:
(1)對所有 a , b , c F,若 a
b,則 a + c
b + c。
(2)對所有 a , b F,若 0
a 及 0
b,則 0
ab。
我們稱 F 為全序域。這個『』更進一步符合我們慣常意義下的不等式之要求。
那麼,複數域是全序域嗎?Justin 的留言已經說明了,複數域不是全序域。讓我也不厭其煩,重述之。
我們用前述的『字典排序』,有 0 i。
假如複數域是全序域,由條件(2),得 0
得 0 -1
有違『字典排序』,生矛盾。
好,若我們在複數域上定義另外的全序(不用『字典排序』),表之曰⊿。由全序定義,我們必有
0 ⊿ i 或 i ⊿ 0 或 i = 0(不合)
先考慮 i ⊿ 0
由全序域的條件(1),得 i + (-i) ⊿ 0 + (-i)
即 0 ⊿ -i
由全序域的條件(2),得 0 ⊿ (-i)(-i)
即 0 ⊿ -1 ———————————- (*)
再由全序域的條件(2),得 0 ⊿ (-1)(-1)
即 0 ⊿ 1
由全序域的條件(1),得 0 + (-1) ⊿ 1 + (-1)
即 -1 ⊿ 0 ———————————– (**)
由 (*) 及 (**) 可見,⊿ 已不符合全序的其中一個條件:三一律,所以我們不能在複數域上定義這種滿足全序域的序 ⊿。
類似地,若考慮 0 ⊿ i,我們也可推導出 ⊿ 有違全序的條件,諸君不妨一試。這樣,正是這個原因,我們會(粗疏地)說『兩個複數可排序但不能比較大小』。
總結
複數集是全序集,但
複數域不是全序域。
至於第三種序:良序。對歸納法之所以可行和研究無限集序數等有重要意義,但和本篇主題不太相關,就此在結。
為何一數大於0,
它的平方就一定要大於0?
它不是序不行嗎?
不滿足這四個性質不能比較大小嗎?
迴響 由 Yee — 2011/10/18 @ 12:40 下午 |
按定義,在全序域某元「大於」零,它自乘必「大於」零。
若你所指的「大於」不是(全?)序時,我不懂了,求教。
「不滿足這四個性質不能比較大小嗎?」
是質疑我用「不能比較大小」這類形容嗎?
如果複數「不能比較大小」的意思是指:
「雖然複數可定義出全序⊿,卻不能滿足 0⊿a & 0⊿b => 0⊿ab,即不能滿足一般實數,按慣常定義下的不等式 < 之特性。」
可以嗎?
迴響 由 johnmayhk — 2011/10/18 @ 5:26 下午 |
不是全序域就不能比較大小嗎?
迴響 由 Yee — 2011/10/18 @ 6:44 下午 |
你認為呢?
迴響 由 johnmayhk — 2011/10/18 @ 8:31 下午 |
我認為可以。
複數沒有不能比較大小的理由。
只是沒有實用的方法。
如果只是為比較而比較也可以。
迴響 由 Yee — 2011/10/18 @ 10:33 下午 |
題外話,
實數比較大小的方法在物理上是否有意義?
1與-2誰大?
沒有人會懷疑,
1 > -2。
請問,
1庫侖正電與2庫侖負電,
哪個電量大?
迴響 由 Yee — 2011/10/18 @ 10:35 下午 |
「1庫侖正電與2庫侖負電,哪個電量大?」在物理學上是如何解答?
迴響 由 johnmayhk — 2011/10/19 @ 11:21 上午 |
課本沒有明確提過,
不知道。
迴響 由 Yee — 2011/10/19 @ 12:21 下午
三度空間中有八個卦限,
但只定義第一卦限。
其它七個卦限不能定義嗎?
沒有定義,
但不是不能定義。
同樣的,
複數也不是不能比較大小。
迴響 由 Yee — 2011/10/20 @ 3:05 下午 |
「可以比較大小」=「可以定義全序」嗎?
迴響 由 johnmayhk — 2011/10/21 @ 6:02 上午 |
剪刀、石頭、布猜拳的遊戲,
如果用數學符號表達,
a>b
b>c
c>a
滿足三一律,
但不滿足遞移律。
不是全序。
你認為猜拳的這種關係不用變成數學模型嗎?
迴響 由 Yee — 2011/10/21 @ 10:05 上午 |
可否總結為:
1.因複數可排序,故複數可比較大小。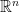 任何兩元都可比較大小。
任何兩元都可比較大小。
2.可數集及
3.諸如 “can’t compare two complex numbers" 的論述是錯的。
(e.g. http://www.cut-the-knot.org/do_you_know/complex_compare.shtml)
回應:
1.對於複數,諸如上述的排序只宜止於比較大小,不宜作「進一步」運算。
比如,縱有
但也可以出現以下情況:
更遑論如實數般解更複雜的「不等式」?
2.應該對中學生說:「複數可比較大小。」
3.是否存在一些集,它的元不能比較大小?
迴響 由 johnmayhk — 2011/10/21 @ 9:44 下午 |
應該說複數不定義比較大小的法則,
而非複數不能比較大小。
迴響 由 Yee — 2011/10/21 @ 10:34 下午 |
何謂"不定義比較大小的法則"?
迴響 由 johnmayhk — 2011/10/21 @ 10:38 下午 |
就是不定義它們的大小關係。
迴響 由 Yee — 2011/10/21 @ 10:41 下午
把猜拳的法則推廣,
它有三個元素0,1,2
大小關係為:
0<1
1<2
2<0
如果擴展至5個元素:0,1,2,3,4
0<1,0<2
1<2,1<3
2<3,2<4
3<4,3<0
4<0,4<1
同理,可以擴展至奇數個元素。
數學上有定義這種東西嗎?
迴響 由 Yee — 2011/10/21 @ 10:40 下午 |
「複數不定義比較大小的法則」而不是「複數不能比較大小」。
「{0,1,2} 可定義比較大小的法則(例如你所謂的猜拳法則)」所以「{0,1,2} 的元可比較大小」
對嗎?
迴響 由 johnmayhk — 2011/10/21 @ 10:58 下午 |
是。
迴響 由 Yee — 2011/10/21 @ 11:07 下午
但為何字典排序不可視作所謂的法則?
怎樣理解「複數可以比較大小」但「複數不定義比較大小的法則」?
迴響 由 johnmayhk — 2011/10/21 @ 11:13 下午 |
字典排序是法則。
只是用在複數上沒有進一步用處,
所以不用。
迴響 由 Yee — 2011/10/22 @ 7:23 上午 |
既然「複數的字典排序是比較大小的法則」何解你說「複數不定義比較大小的法則」?
迴響 由 johnmayhk — 2011/10/22 @ 8:10 上午 |
這是可行的方法,
但沒有人採用,
大家選擇不定義。
迴響 由 Yee — 2011/10/22 @ 10:38 下午
讓我玩一玩(不用認真):
小明有一億萬元,小強有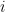 元,哪人有的錢比較多?
元,哪人有的錢比較多?
A.不能比較
B.小明
C.小強
迴響 由 johnmayhk — 2011/10/22 @ 8:20 上午 |
換一個說法,
可以定義,
但因為沒有定義,
所以不知如何比較,
所以無法比較。
迴響 由 Yee — 2011/10/22 @ 10:44 下午 |
「猜拳法則」不是數學上定義的「序」。
「猜拳法則」卻是一種「比較大小」的「法則」。
「字典排序」是數學上定義的「序」。
「字典排序」也可以是一種「比較大小」的「法則」。
那麼,符不符合數學上定義的「序」,也可以是「比較大小」的「法則」,對嗎?
回到最基本問題:何謂「比較大小」?
複數可以「比較大小」是因為諸如字典排序可被定義,對嗎?
你說過「為比較而比較」是可以的。
即是說,不理會那種法則有否在某些範疇(諸如數學上或物理上)的應用,不理會有沒有人採用,定義到「比較大小」的法則是可以了。
這樣,「比較大小」是甚麼?
「比較大小」是二元關係的一種( ),但似乎我們不會認為,二元關係就是「比較大小」吧?
),但似乎我們不會認為,二元關係就是「比較大小」吧?
那麼,「猜拳法則」是「比較大小」的法則的理由是甚麼?
迴響 由 johnmayhk — 2011/10/23 @ 7:46 上午 |
數學建構出許多模型,
是為了討論方便。
猜拳是為了分勝負,
分勝負與比較大小的觀念一致。
你認為猜拳不能變成一種數學模型嗎?
迴響 由 Yee — 2011/10/23 @ 8:50 上午 |
我要問「分勝負與比較大小的觀念一致」嗎?
在猜拳遊戲中,因為布「勝」石頭,所以有人認為布「大於」石頭。
在鬥獸棋中,因為鼠「勝」大象,所以有人認為鼠「大於」大象。
但在實數中,人認為 2 大於 1,似乎和「勝負」關係不大。
和前兩例不同,2 大於 1,涉及比較數值上的大小,或(更原始地)比較數量上的多少。
人不一定以數學(模型)界定勝負,常識也。
諸如政治上的權力、選美上的美醜,不一定可以量化,更不易定義當中的「四則運算」,可是,人也能人為地去定義決勝的方法,從而可以界定「大小」。
若以數學述語描述,人若認為「勝」、「吃」(下棋時)、「在…之先」、「在…之上」等,和「大於」的觀念「一致」,似乎因為它們不過是「符合三一律的二元關係」。
若不談論數值上的大小,不作進一步的運算,只為比較而比較,為定勝負而定勝負,那麼,只要在某集上定義出符合三一律的二元關係,則該集的任何元都被認為是可以「比較大小」。
可以比較「布和石頭」的「大小」,就沒有不可以比較複數「大小」的理由。
然而,若「比較大小」是涉及比較數值上的大小(數量之多少),那麼「比較大小」所描述的性質是否應該更多?
起碼有諸如「若 A 較 B 多及 B 較 C 多,可知 A 較 C 多」的性質吧。
不同於「布、剪刀、石頭」,複數涉及數值,且存在類似實數的四則運算。
若討論數值,「全序」似乎較符合「比較數值上的大小」的性質或法則(起碼包括傳遞性)。
若討論四則運算,實數進行運算後,數值上的「大小」有一定會符合某些性質,諸如由「a 大於 b 及 c 大於零」,必然存在「ac 大於 bc 這個結論」。「全序域」就是考慮這樣的比較數值大小的條件。
假設複數可以如此比較數值大小,但如內文所指,總存在一些運算,導生矛盾。從而逆推出,甚至是以全序域這種比較數值大小的條件法則,對複數值,也是不適當。故有人認為不可以比較複數(數值上的)大小。
不懂回答「猜拳不能變成一種數學模型嗎?」,因我不太明白「變成一種數學模型」是甚麼意思。可以用一些數學術語來描述是否就「變成一種數學模型」呢?比如我說,「鬥獸棋法則」是符合三一律的二元關係,我算不算用一些數學術語來描述「鬥獸棋法則」呢?如果算,那麼鬥獸棋法則就變成一種數學模型了。對嗎?
還是「猜拳不能變成一種數學模型嗎?」其實是問「一定以數學(模型)界定大小嗎?」如是者,當然不是。
迴響 由 johnmayhk — 2011/10/23 @ 11:15 下午 |
理論都是人寫出來的,
就看你覺得合不合理。
只是你覺得不合理,
我覺得合理而已。
迴響 由 Yee — 2011/10/24 @ 9:37 上午
你認為分勝負與比較大小無關,
我也不能說有什麼不對。
迴響 由 Yee — 2011/10/24 @ 9:39 上午
Ref comment 15
1.對,有人認為「鼠大於象」是合理,有人不然。這都是人為定的。
2.我並非認為「分勝負與比較大小無關」,勿誤會。
迴響 由 johnmayhk — 2011/10/24 @ 10:49 上午 |
突發奇想:
正正得正不成立,
所得到的結論為什麼是虚數無法比較大小,
而不是虚數不存在?
迴響 由 Yee — 2011/10/24 @ 12:12 下午 |