這是有關「可導性」(differentiablity)的討論,寫給那天沒有上復活假期補課班的中六同學。注:討論純粹以中學數學的觀點出發。
先請同學回答下面三道是非題:
1. Put into the expression of
and it is undefined, then
is not differentiable at
. True?
2. If , then
is differentiable at
. True?
3. If is finite, then the value of
is also finite. True?
=======================================
上面三題的答案皆「不一定是」。
=======================================
首先,要描述一個函數是否「可導」(differentiable),我們不是看 這個表達式是什麼,最安全的,都是返回「可導」的定義。
再看看上述的三題
Question 1:
代 入表達式
,而「計不到數」(undefined),並不一定代表”
is not differentiable at
”.
以下是一個經典的例子:
for
and
.
對於 ,恆有:
– – – – – – (*)
若把 代入上式 (*),但因為當
,
是「計不到數」(沒有定義 undefined),同學往往以為
在
處也是 undefined,故他們聲稱”
is not differentiable”。
錯!
判別「可導」與否,一定要回歸「可導」的定義:
” is differentiable at
”的意思是「極限
存在」。
一旦極限存在,我們才可寫 ,而並不是先用中四五的手法,找出
的表達式,再代入
,就得出
。
返回那經典例子:
for
and
.
當我們考慮極限
根據定義,
,
,故
因 有界(bounded),且
,故
,即
亦即此極限存在(等於 0,即 )是故
is differentiable at
Question 2 和 Question 3 可以一併考慮,隨便舉例
for
and
for
對於 ,我們易知
for
and
for
易知
於是
但,明顯地, 在
之處是不可導(not differentiable at
)。
最簡單的原因是, 在
之處根本不連續(not continuous at
),見下
可見
是故 在
之處不連續,從而不可導。
現在,具體地計算一下 在
處的左導數(left-hand derivative),即
左導數不存在,導數也自然地不存在,順便回答了 Question 3:
(finite)但
(infinite)
重申一次,縱使存在以下關係:
我們也不能知道 存在與否,
亦即不能保證 在
之處是可導。
習題
1. Let
for
and
for
Suppose is differentiable at
, evaluate
.
2. Let
for
and
for
Will be differentiable at
for some real number
?
3. Let
for
and
for
Given that is differentiable at
.
Is is true to write ””?
sir, here is my ans:
1. a=+1
2. differentiable when b=+1
3. T
but i actually don’t know what exactly what f'(x) is
what is the different in meaning between
lim f'(x)
x->0-
and
lim (f(h)-f(0))/h
h->o-
and also
lim f(x)
x->0-
i don’t know which one to consider when doing calculation
迴響 由 harrison — 2009/04/17 @ 8:16 下午 |
Harrison,
The answer to Q.2 is FALSE.
Just think about the graph of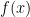 , it is ALWAYS discontinuous at
, it is ALWAYS discontinuous at  (even for
(even for  ). (Or prove it by simple algebraic computation)
). (Or prove it by simple algebraic computation)
What is ?
?
It is a limit.
By definition,
If the limit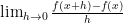 EXISTS, we define it as
EXISTS, we define it as
What is ?
?
It is NOT in general.
in general.
By the definition above,
hence
You see, it is NOT in general, because, by the definition,
in general, because, by the definition,  is simply:
is simply:
SOMETIMES, is really equal to
is really equal to  , as for example, when the function
, as for example, when the function  is continuous at
is continuous at  .
.
Also, can you prove that the answer to Q.3 is TRUE?
迴響 由 johnmayhk — 2009/04/18 @ 6:12 下午 |
For Question 1, I used to teach my students in the same way as yours before at the beginning, but later I found that the answer of Q1 is true, and I also got a very simple proof.
Let me first point out the problem of your counter-example.
If f(x) = x^2 sin 1/x if x is not 0 and f(0) = 0,
then what is f'(x)?
Answer:
f'(x) = (the expression you have) if x is not 0 and f'(0) = 0
Therefore, when we put x = 0 , f'(0) = 0 which is defined.
[ What you showed in your counter-example is in fact,
lim {x -> 0} f'(x) . ]
Back to the proof of the statement.
Assume f(x) is differentiable at x = 0.
Then f'(0) exists (defined), which leads to a contradiction.
Therefore f'(x) is not differentiable at x = 0.
迴響 由 Cheng Wing Kuen — 2009/04/21 @ 8:09 上午 |
Thank you Cheng Wing Kuen.
是我的表達出了問題。
在 Question 1 中,
Put into the expression of
into the expression of 
當中我希望說的,不是 。
。
當中的 expression,其實指,把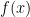 進行求導後得出的 expression。
進行求導後得出的 expression。
如上例
利用求導法,得出的 expression 就是
Question 1 想說的,就是 put into the expression above.
into the expression above.
它是 undefined 的。
它不是 。
。
我只是想指出,同學往往誤以為
「把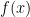 D 完,再代個零入去,計唔到,就即係函數係 x = 0 個位 D 唔到」。
D 完,再代個零入去,計唔到,就即係函數係 x = 0 個位 D 唔到」。
是我的表達出問題,”expression of ”確實可以指
”確實可以指
那麼,當”Put into the expression of
into the expression of  ” 就被理解為
” 就被理解為  時,
時,
誠如 Cheng Wing Kuen 所言,
Question 1 is trivially true.
We can prove it simply by contrapositivity.
“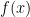 is differentiable at
is differentiable at 
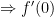 exists"
exists"
is equivalent to
“ does not exist
does not exist  is not differentiable at
is not differentiable at  "
"
P.S.
Oh, Mr. cheng, are you the writer of “永權網頁"? I love the website, it is very useful.
迴響 由 johnmayhk — 2009/04/21 @ 2:46 下午 |