中二數學堂。
同學甲:「零的零次方是什麼?」
同學乙:「1,中一教過,任何數的零次方都是 1。」
同學丙:「零的零次方係計唔到。」
我:「點解計唔到?」
同學丙:「你試下用部 Calculator 計下,math error 啦!」
我:「點解計唔到?」
同學丙:「因為 math error,中一阿 sir 係咁解。」
同學乙:「點解書話:任何數的零次方都是 1?」
(虛擬人物)同學丁:「答案是 0,因為 0 的任何次方都是 0。」
係時候秒殺之,我立即寫了幾步:
再問同學,咁大家認為
是什麼?
眾曰:「zero over zero」
那麼,「zero over zero」是什麼?
某某曰:「計唔到。」
其實我並沒有說得太詳細,一來之前和他們談過為何零不能做分母,二來,始終他們是中二的同學,於是一句「 is undefined」作結。
不過,必須澄清,「任何數的零次方都是 1」是錯的。
中二同學,我們應該說,「任何非零的數,其零次方都是 1」。
可以繼續和同學玩,著他們用計算機找找以下的答案,看看他們可以得出什麼樣的結論:
如果試試負數,比如 又怎樣。
修純數的同學,當然可以完全 KO。但,不要忘記,他們只是中二同學。
之前我也教過這個課題,不過我們是在中三才學整數指數定律。也有同學問過「零的零次方」問題,也是輕輕帶過說是「undefined (未定義)」。對於初中同學來說,解釋起來有點費力。反而用「Division Algorithm」來解釋「為何不能除零?」,他們又聽得明白喎。
迴響 由 Kam — 2008/10/23 @ 10:44 下午 |
0=0^1=0^(2-1)=0^2/0^1=0/0
所以0是未定義的?
迴響 由 Yee — 2008/11/04 @ 6:55 下午 |
Yee,頗有趣的「證明」唷。
不過致命傷在
0^(2-1) = 0^2/0^1
這步。
Remark: Index law “ " is invalid for
" is invalid for  .
.
所以 Yee 可能已看出我當天用 作解釋是不妥當的,但,我也要說,他們不過是中二同學。
作解釋是不妥當的,但,我也要說,他們不過是中二同學。
迴響 由 johnmayhk — 2008/11/04 @ 9:58 下午 |
不要說是對中二的學生,就算是專業的數學家也無法推翻0^0=1的說法,頂多只能說它應用的地方不夠多,所以不去定義。
至於它應用的地方雖然不多,但仍然找得到。
迴響 由 Yee — 2008/11/05 @ 10:03 上午 |
確實,我們可以定義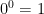 ,或許是這樣的定義是比較「方便」。
,或許是這樣的定義是比較「方便」。
比如,設無窮級數
我們知道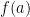 應該是
應該是 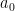 。
。
若把無窮級數表達成
看看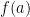 ,出現了
,出現了  ,那麼我們要
,那麼我們要 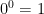 。
。
當然,修純數的同學比較熟識以 l’ Hôpital rule 得到
為使 也連續於
也連續於  ,最正常是定義
,最正常是定義 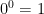 。
。
不過,最簡單的看 ,我們不也可定義
,我們不也可定義  嗎?
嗎?
如果不考慮剛才的 ,而是
,而是  的話,那麼無論怎樣定義,
的話,那麼無論怎樣定義, 不可能於
不可能於 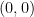 連續。
連續。
迴響 由 johnmayhk — 2008/11/05 @ 11:28 下午 |
你的論點有一個很大的盲點:不連續就不能定義嗎?
不連續照樣可以定義,沒有矛盾。
至於定義它的意義在哪裡?在別的地方用得到。
一、令0^0=x
對任意數k,x^k=(0^0)^k=0^(0*k)=0^0=x
其中k可以為負數,此時0不是解。所以1是唯一解,意即1是0^0唯一合理的定義。
二、在組合數學中,將n相異物分給m人的方法有m^n種,當n=0,不用分就可完成,本身就是一種方法。例如0!為0物作直線排列,C(0,0)為從0物中取0物的組合數都是1種方法,所以將0物分給0人也是1種方法。
迴響 由 Yee — 2008/11/06 @ 8:53 上午 |
非常感謝 Yee 的留言,令在下開了眼界,謝謝!
在下仍是認為:為了「方便」,定義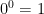 是一種「合理」的「選擇」。
是一種「合理」的「選擇」。
這個方便,可以是
1. 使 (如 comment 5 的例)
(如 comment 5 的例) 在 [0,+
在 [0,+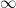 ) 上連續(如 comment 5 的例
) 上連續(如 comment 5 的例  )
)
2. 使
當然,誠如 Yee 所言,就算在某處不連續,函數仍然可以在該處有定義。我只是想說,連續性不一定是迫使我們定義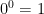 的理由而已。
的理由而已。
3. 使「 相異物分給
相異物分給  人的方法有
人的方法有  種」這公式在
種」這公式在  時仍然可用。
時仍然可用。
正如 Yee 提及的 ,就是原本
,就是原本 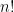 被定義為首
被定義為首  個連續正整數的乘積,擴充到
個連續正整數的乘積,擴充到  時,定義
時,定義 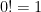 是最合理,起碼合 「
是最合理,起碼合 「 」 之理。但我們知道
」 之理。但我們知道  並非「金科玉律」,起碼當
並非「金科玉律」,起碼當  時,它是不成立的。
時,它是不成立的。
4. 使 Index law 可應用的範圍被擴充
a. 比如我們不用寫「 for
for 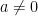 」而直接寫「
」而直接寫「 for any
for any 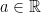 」
」
不過,這個說法,我們可以得到平行的看法:我們不用寫「 for
for 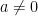 」而直接寫「
」而直接寫「 for any
for any 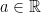 」
」
b. 比如 在
在  時仍然可行(即 Yee 的例)。
時仍然可行(即 Yee 的例)。
但,我們接納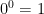 ,又把 Index law 的應用範圍擴充,那麼會否產生另一些問題?比如
,又把 Index law 的應用範圍擴充,那麼會否產生另一些問題?比如
Yee 在 comment 2 的反問「所以 0 未被定義?」用到
另一方面,讓我詳細看清楚 Yee 的例子 1。
令
 ,
, – – – (1)
– – – (1)



 可以為負數,此時 0 不是解。- – – (2)
可以為負數,此時 0 不是解。- – – (2) 唯一合理的定義。
唯一合理的定義。
對任意數
其中
所以 1 是唯一解,
意即 1 是
基於 (1), 可以是任意數,
可以是任意數, 可以是負數」,
可以是負數」, 的解。
的解。
所以得 (2) 當中的論述:「
從而 0 不是
問題是,(1) 已經一早預設了「 不是零」這個我們想推出的結果。
不是零」這個我們想推出的結果。
因為當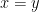 ,要「對任意數
,要「對任意數  ,包括負數
,包括負數  」,使「
」,使「 」成立的先決條件要:
」成立的先決條件要: 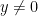 。
。
那麼,這會否為求達到 (這個起初仍未被定義的東西)等於 1 這個目的,而先「老屈」它不是零,從而推論出合乎我們意願的結果?證明有否循環論證之嫌?
(這個起初仍未被定義的東西)等於 1 這個目的,而先「老屈」它不是零,從而推論出合乎我們意願的結果?證明有否循環論證之嫌?
順帶說, 的解,除了有 1,0 還可以有別的複數。
的解,除了有 1,0 還可以有別的複數。[OT] Yee,你是我的舊同事 Yee(余師傅)嗎?
迴響 由 johnmayhk — 2008/11/06 @ 12:16 下午 |
一、
我不認為這個定義是為了方便,而是為了事實,定義只是承認已經存在的事實。
二、
指數律遇到分母為0或0的負數次方時不適用。
0=0^1=0^(2-1)無誤。
但0^(2-1)=0^2/0^1這一步,遇到了分母為0,不適用,所以不成立。
這個限制可以解決另一個問題:
1^0/0^0=1/1=1
1^0/0^0=(1/0)^0
是否遇到(1/0)^0=1的問題?
不會,1^0/0^0=1/1=1無誤,但1^0/0^0=(1/0)^0遇到分母為0,不成立。
三、
0^0與0/0並沒有關係,不要拿否定0/0的理由來否定0^0。
1=2是0/0的矛盾,不是0^0的矛盾。
四、
我一開始並未預設0^0不可為0,但是在運算過程中,並未遇到指數律不成立的條件,所以繼續成立,把0排除在外。
x^(-1)=x的解,只有1與-1,沒有其它複數。
五、
我不是你的舊同事。
迴響 由 Yee — 2008/11/06 @ 12:48 下午 |
即使是解x^2=x,也只會得到0與1,不會得到別的複數解。
迴響 由 Yee — 2008/11/06 @ 2:35 下午 |
1. 如果「 」成立,不就暗示了
」成立,不就暗示了 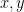 皆非零嗎?
皆非零嗎? = 那個原先不知為何物的東西
= 那個原先不知為何物的東西  ,情況一:當
,情況一:當 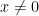 時,「
時,「 」成立,之後即是 Yee 提供的證明。情況二:當
」成立,之後即是 Yee 提供的證明。情況二:當  時,不過是取
時,不過是取 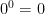 之意
之意 ,竟然可以知道它符合指數律:
,竟然可以知道它符合指數律: !有問題嗎?
!有問題嗎? ,純粹仿效 Yee 在 comment 2 的手法而已。誠如 Yee 所言,
,純粹仿效 Yee 在 comment 2 的手法而已。誠如 Yee 所言, 對支持或推翻
對支持或推翻 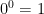 並毫作用。
並毫作用。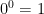 是一個事實」,在下認為「
是一個事實」,在下認為「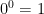 是一個『被定義出來』的『事實』」正如『0! = 1』是一個『事實』。
是一個『被定義出來』的『事實』」正如『0! = 1』是一個『事實』。
2. 證明是否應該分兩個情況?設
,亦同樣得到 這個效果
這個效果。3. 一個原先不知為何物的東西
4. 我玩
5. Yee 認為「
迴響 由 johnmayhk — 2008/11/06 @ 3:06 下午 |
1、
這是用等量公理來成立,但我還看不出與本題有何關聯。
2、3、
在我的推論中,完全沒有遇到分母為0或0的負數次方,沒有理由不用指數律。
至於你認為0^0=0的可能性可以從這裡推翻。
如果不從這裡推翻,0^0=0在其它領域找不到印證,所以不採取這個定義。
4、
我推出0=0/0,說明不能用錯誤的理由推翻0^0=1。
5、
這是一個比較觀念性的東西,你不認同也無所謂。
0!=1,究竟是因為有了這個定義才成立,還是有了這個事實才定義?
如果你選擇前者,0!也可以不定義,也可以定義為其它值嗎?
如果你選擇後者,0^0可以不定義為1嗎?
迴響 由 Yee — 2008/11/06 @ 5:17 下午 |
上面第1點刪掉。
迴響 由 Yee — 2008/11/06 @ 5:46 下午 |
0^0 不是1
因為無連續性
0^(0.001)=0
0^(-0.001)= 無限大
無限大跟零之間﹐突然有個1
不合理。
0^0次方為任何數﹐非僅1
迴響 由 mirapc2002 — 2009/04/14 @ 7:26 下午 |
不連續不足以作為不定義之理由。
迴響 由 Yee — 2009/04/28 @ 12:54 下午 |
可以参考一下wikipedia有關0^0的內容
http://en.wikipedia.org/wiki/0%5E0#Zero_to_the_zero_power
入面有一句According to Benson (1999), “The choice whether to define 0^0 is based on convenience, not on correctness."
迴響 由 stupid girl — 2009/05/07 @ 11:41 下午 |
這我老早就看過了。
這個論點我無法接受。
不定義的理由就是這麼荒謬。
迴響 由 Yee — 2009/05/08 @ 8:57 上午 |
Maths is all definitions. The question is how you define your things so that they work for you. As for 0!, notice that n! can be analytically continued to the gamma function, Gamma(1)=1.
迴響 由 H — 2009/05/14 @ 3:05 上午 |
I have mentioned that discontinuity is not the reason not to define.
We can find some reasons to define, but we cannot find any reason not to define, why don’t we define it?
What about not defining 0?
迴響 由 Yee — 2009/05/14 @ 9:02 上午 |
Maths is all definitions and 0^0 must be defined as 1 and works well.
Reasons in Chinese is in previous articles.
This definition is irrelevant to continuity.
迴響 由 Yee — 2009/05/15 @ 8:18 上午 |
都半年多了還在討論零的零次嗎?
我已經找到你的証明的漏洞了,想不到你還在堅持
“令0^0=x
對任意數k,x^k=(0^0)^k=0^(0*k)=0^0=x"
x^k=(0^0)^k是對的,0^(0*k)=0^0=也是對的,
但(0^0)^k=0^(0*k)用了law of indices, 但其公式只給non-zero base定義
你只定義了0^0存在,並不允許zero-base的運算,故些証明不精確
“在組合數學中,將n相異物分給m人的方法有m^n種,
當n=0,不用分就可完成,本身就是一種方法。
例如0!為0物作直線排列,C(0,0)為從0物中取0物的組合數都是1種方法,所以將0物分給0人也是1種方法"
0物分給0人為甚麼是一種?實際上沒有可能發生的事為甚麼出現了一種情況?
要說C(0,0)是因為有定義了0!=1才等於1。要說明顯先 “証明" 0!吧
你是學會nCr後才懂分物件嗎?
那麼0物分給1人為甚麼不是一種?因為沒有C(0,1)?
雖然yee認為limit 有contradiction 不等於該數值不能被定義我十分認同,
但在我認知的數學中並沒有一種方法可直接找出該數值,概念誠然與0除0一樣
引用Universirty of Utah , Peter Alfeld在 証明0除0時的一個重點:
“the result of a division by zero is undefined is the fact that any attempt at a definition leads to a contradiction"
我並不認同你說專業的數學家也無法推翻0^0=1的說法,
反之我認為不倚賴limit的話,專業的數學家也無法寫出0^0=1的証明呢!
記得半年前yee是認為若不定義0的0次有欠完美
剛剛在做我的畢業習作,發現0除0不能被定義的証明也是有漏洞的,只是個安撫學生的謊言
悍衛數學完整性但不認同limit的你何不把它一併証明?
迴響 由 Asathor — 2009/05/27 @ 3:26 上午 |
底數為0時指數律仍可適用。
0^2*0^3=0^(2+3)
(0^2)^3=0^(2*3)
只有當遇到0的負數次方或分母為0時才不適用。
如果你認為底數為0時指數律完全不適用,請問0^2如何定義?
0物分給0人為什麼是1種?因為東西分完了,所以是1種方法。
n!是n物作直線排列的方法數,0!是0物作直線排列的方法數,0!=1,意即0物作直線排列有1種方法,這種方法就是什麼都不做,而東西都已經排好了。0^0=1也是同樣的道理。
0物分給1人的方法數,是1^0=1。
以上我只能當成定義的理由,而非證明。
專業的數學家也找不出定義0^0=1的矛盾。
有人說在不連續點上給予定義是不優雅的修補而不該做。
有人說定義0^0與否取決於方便性而非正確性。
我沒有找到任何文章舉出矛盾。
令0/0=x,
2*x=2*0/0=0/0=x,x=0
1/x=0/0=x,x=1,-1
二者無交集,x無解,0/0無法定義。
這個證明你滿意嗎?
迴響 由 Yee — 2009/05/29 @ 9:45 上午 |
底數為0時指數律不適用。
0^2是單純可解讀為0x0, 故看似和指數律吻合,不能因此默認指數律包括base0
cobination 是以 概率的 possible outcome/flavourable outcome 為基礎的
故C(0,0)是為完整性而加的,並不含有意義,因flavourable outcome 是零的話,
會引申成0/0的問題
let 0/0= X, 不代表能運算, 不代表 0/0 = (0x2)/0
(0x3)/0= 0/0 = (0x2)/0
3 x (0/0)=2 x (0/0)
X=0/0 唯有=0
那麼1/x何來成立呢? 何來等於0/0呢?
1/(0/0)我看不懂為何可以寫成0/0
1/x 要先假設X非零,和以上矛盾
故無法導出 X= 1or -1
so X=0/0=0, lead to contradiction
迴響 由 Asathor — 2009/06/02 @ 1:55 上午 |
若0物分給0人能寫出0^0這種組合的話,
為什麼就寫不出也是形容0物分給0人的0/0呢?
迴響 由 Asathor — 2009/06/02 @ 1:58 上午 |
Concept of fraction is based on multiplicative inverse
The ratio r of two numbers a and b: a/b=r
is that number r that satisfies a=r x b
if 0/0 exist, let say z. z would have to satisfy z x 0=0.
all real z satisfy the above equation
so your proof should not start with a fixed constant x.
ref:http://www.math.utah.edu/~pa/math/0by0.html
迴響 由 Asathor — 2009/06/02 @ 2:25 上午 |
既然吻合為何為不適用指數律?
允許定義0^2,卻不允許使用指數律的理由何在?
所有的定理定律,都希望適用範圍能夠最大,你卻反其道而行,要讓適用範圍變小。為了不定義0^0嗎?
C(0,0)為什麼沒有意義?0都已經定義幾個世紀了,你還不能接受0個東西這種說法嗎?
引申成0/0的問題是什麼問題?
“若0物分給0人能寫出0^0這種組合的話,為什麼就寫不出也是形容0物分給0人的0/0呢?"
n物分給m人的方法數為m^n。
n物平分給m人,每人得到的個數為n/m,並且這種東西還要能分割。
不知道你要憑什麼寫成0/0?
迴響 由 Yee — 2009/06/02 @ 6:11 下午 |
全部適用才叫適用哦
0^0=0^(4-4)=0^4/0^4=0/0嗎?
適用指數律是指一條, 兩條嗎?
1=x^0=(0^0)^0=0^(0^0)=0^x=0^1=0 夠奇怪吧
要是適用的話你便不用迴避這寫法了
莫非為了方便你而加個exception?
全世界的數學書也寫n!是 n greater or equal to 1的, 0!是定義
莫非n項物品環形排列有(n-1)!
0項物品環形排列有(-1)! ?
意義是推論,但不代表合邏輯
0物分給0人已經沒有邏輯了,能作証明嗎?
0物平分給0人,每人得到的個數為0/0, 對街上的人不是理所當然嗎?但你不知道憑什麼寫成這樣
正如我不能理解0物分給0人能寫出0^0一樣
n物分給m人的方法數為m^n
0物平分給4 人 4^0=1
0物平分給3 人 3^0=1
0物平分給2 人 2^0=1
0物平分給1 人 1^0=1
0物平分給0 人 0^0=1 看似很合理
如果0物平分給0 人,即分給0人這一行徑有意義的話,那為何
4物平分給0 人 0^4=0
3物平分給0 人 0^3=0
2物平分給0 人 0^2=0
1物平分給0 人 0^1=0 時
0物平分給0 人 0^0=1 呢?
那你試以一根沒有長度的尺量度一條沒有長度的橋吧!
只用言語很難說服人為何0^0應有數字而0/0沒有吧!
迴響 由 Asathor — 2009/06/04 @ 2:17 上午 |
指數律遇到0的負數次方或分母為0才不適用,其它情形都是適用的,包括底數為0。
你要定義0^2,又不讓指數律適用,這是很奇怪的。
0!=1是定義,0^0也應該定義為1。
n物分給m人的方法數為m^n
4物分(不是平分)給0 人,無法找出一種方法找東西分完,是0種方法,符合 0^4=0。
0物分給0人,一開始就已經分完了,所以是1種方法。
能分完的才是方法,不能分完的就不是方法。
迴響 由 Yee — 2009/06/04 @ 9:11 上午 |
“1=x^0=(0^0)^0=0^(0^0)=0^x=0^1=0"
你已經令x=0^0
你錯在(0^0)^0=0^(0^0)這一步,
應該改為(0^0)^0=0^(0*0)=0^0
你寫錯了當然奇怪。
寫對了就不奇怪。
迴響 由 Yee — 2009/06/04 @ 9:15 上午 |
真的寫錯了
但0^0=0^(4-4)=0^4/0^4=0/0也是不能迴避的
以下的logical prove 應該沒問題了
Let 0 be applicable to law of index,
Let x=0^0
For all k, x^k=(0^0)^k=0^(0*k)=0^0=x
imply x=1, i.e. 0^0=1
then 1=0^0=0^(4-4)=0^4/0^4=0/0
which lead contradiction!
So 1=/=0^0
(0^0)^k=0^(0*k)=0^0 for all k,
imply 0/0=1 but 1 =/= 0/0
Contradiction!
Thus 0 is not applicable to law of index.
語言遊戲是玩不完的了
“0物分給0人,一開始就已經分完了"也不能証明是vaild stament
我的家產分給0人就是不分給人, 我有家產或無不重要,
Quamtum machenic 中 Schrödinger’s Cat 的原理也是一樣,
不去分根本不需理會本身有沒有東西,
0物平分給4 人
0物平分給3 人
0物平分給2 人
0物平分給1 人 也有動作, 每人0個
0物平分給0 人 有給的意義嗎? 能解釋給學生聽嗎?
我有4物分給0 人 分不了因沒有人要
我有3物分給0 人 分不了因沒有人要
我有2物分給0 人 分不了因沒有人要
我有1物分給0 人 分不了因沒有人要
我沒有物品, 分給0 人 竟然是分完了?難道精神分裂? 能解釋給學生聽嗎?
0^0在數學運算中有0物平分給0人的情況嗎?
l’hospital 中的0^0又是有0物分給0人的意思嗎?
迴響 由 Asathor — 2009/06/05 @ 9:58 下午 |
不能迴避?
我已經說明了指數律不適用,就解決了這個問題,你怎麼一直抓著不放?
遇到0的負數次方和分母為0時才不適用,否則仍然適用。
你說0^0=0^(4-4)=0^4/0^4=0/0
那麼0=0^1=0^(2-1)=0^2/0^1=0/0,所以連0都不能定義了!
至於我用的x^k=(0^0)^k=0^(0*k)=0^0=x並沒有遇到不適用的情形。
請把我解釋過的看清楚再來討論吧。
“0物平分給1 人 也有動作, 每人0個
0物平分給0 人 有給的意義嗎? 能解釋給學生聽嗎?"
你說的平分,每個人得的個數,是解釋0/0無意義,當然無意義。
“我有4物分給0 人 分不了因沒有人要
我沒有物品, 分給0 人 竟然是分完了"
有東西沒人要,無法分完,當然是0種方法。
0個就是不用分就已經分完了,分完了就是1種方法。
應該沒有這麼難懂吧。
“0^0在數學運算中有0物平分給0人的情況嗎?
l’hospital 中的0^0又是有0物分給0人的意思嗎? ?"
首先,我已經允糾正過你了,是分的方法數,不是平方的個數,你怎麼一直都混在一起?
再來,公式代入都符合,為什麼要當作沒這個意思?
至於l’hospital是求取極限,而定義0^0=1與極限無關。
我只是在重複前面解釋過的。
迴響 由 Yee — 2009/06/06 @ 5:42 下午 |
“遇到0的負數次方和分母為0時才不適用,否則仍然適用"是誰說的?
算了,指數律重點是次方的數字的通用性,
指數律base的數字本身是負數也有問題,
故指數m,n能滿足any number, 這才是它珍貴的地方阿!
用一個domain沒有負數的0^x function硬放進去還說沒問題
放棄了指數律的通用性, 你的理論得來不易哦
迴響 由 Asathor — 2009/06/07 @ 5:02 下午 |
“遇到0的負數次方和分母為0時才不適用,否則仍然適用”這是最合理的解釋。
指數律本來就有限制,指數律之所以不通用,還是0的問題,這個適用範圍是最合理的,有最大範圍的適用性。
如果你限制底數為0時指數律完全不適用,則它更沒有通用性,難道要把指數律整個廢掉?
不了解你提出通用性的目的為何。
迴響 由 Yee — 2009/06/07 @ 10:56 下午 |
如果真要像你所提的通用性,
0的負數次方不能定義,那為何要定義0的正數次方?
乾脆0的次方數全部不要定義好了。
迴響 由 Yee — 2009/06/08 @ 12:37 下午 |
既然這問題已經發生了好一段時間而顯然無法達到共同結論,為什麼不讓它繼續下去呢?以2方的觀點來延續出數學理論,等到長到某一程度自然可看出輪廓,這樣或許能得到更重要的數學理論~
我只是個做作業的學生碰到這問題剛好有疑惑:
那題是這樣:
lim_n->infinity 0^(1/n)=?
if lim_n->infinity 0^(1/n)=1
照極限的定義:
take epison=1/2
卻找不到任何自然數n
使 |0^(1/n) – 1|< 1/2
而這在定極限值為0時不會矛盾
這樣我難免會懷疑:為什麼要定1?
迴響 由 白木耳 — 2009/11/18 @ 10:40 下午 |
關於你所提的論點,在於極限不存在。
極限不存在不代表函數值不能定義,它只是一個不連續點而已。
你的理由沒有理論基礎。
定義的理由上面已經提過了,不定義的理由完全找不到。
為什麼不定義。
0!不要定義好不好?甚至連0都不要定義好了。
迴響 由 yee3816547290 — 2009/11/19 @ 12:48 下午 |
牛頓已經證明了
when n is positive integer,
(a+b)^n=(nC0)a^n*b^0+(nC1)a^(n-1)b^1+…+(nCn)a^0*b^n
那麼,
(1+0)^1=(1C0)(1^1)(0^0)+(1C1)(1^0)(0^1)
1=0^0
除非你能推翻binomial…否則這個證明應該是十分好的
迴響 由 roviury — 2010/01/14 @ 10:42 下午 |
這應該只能算是定義理由的說明,並不是證明。
定義是不能證明的。
迴響 由 Yee — 2010/01/21 @ 10:24 下午 |
0的0次方
跟0/0一樣
無意義
你先去搞懂0/0
自然就會推出0的零次方為何無意義
迴響 由 mirapc200 — 2010/07/29 @ 4:40 下午 |
把0^0視為0/0是錯誤的觀念。
0/0無法找出唯一的合理的值;
0^0定義為1是合理的。
迴響 由 Yee — 2010/08/06 @ 12:31 下午 |
若 0^0 = 1 那麼不就變成了:
a. 0^0 = 1
ln(1)=0*ln(0)
0=0*ln(0)
左方為0, 右方為未下定義?
b. 0^0 = 1
0=log 1 base 0 = ln(1)/ln(0)
0 = 0/ln(0)
左方為0, 右方為未下定義?
c. 0^0 = 1
1 = 1/1 = 1/(0^0)
1 = (1/0)^0?
左方為1, 右方又是未下定義?
其實定義0^0 = 1 純綷為使到 x^x 在 x=0 為連續
但在用的時候卻又諸多掣肘,要經常擔心式中的 1 會否變成 0^0 而使得數字變undefined,失去了定義的意義
不像0!, 1^0, e^i 等可以豐富我們數學運算及知識,那麼是否值得去定義
0^0 = 1 嗎?
順帶一問,我們有定義
ln 0, argument 0, degree (0) 嗎?
迴響 由 Mark Shea — 2011/05/18 @ 10:35 下午 |
一、
ln(a^b)=b*ln(a)
是當a不為0時才成立。
沒有理由支持可以寫出ln(0^0)=0*ln(0)這種式子。
二、
指數律遇到分母為0或0的負數次方不能成立,
也沒有理由支持
1^0/0^0=(1/0)^0這種式子。
三、
誰跟你說定義的理由只是為了讓x^x在x=0連續?
你這樣認為,實在是低估了支持0^0=1者的程度了吧。
極限存在,函數值未必要定義為極限值。
同樣的,極限不存在,也不代表函數值不能定義。
因為極限值不存在就不定義函數值,
是以為數學只剩下分析,沒有別的領域了嗎?
這正是目前大多數數學家不定義0^0=1的理由。
四、
不定義0^0=1的結果,
在討論多項式(包含泰勒展開式)時,
常數項要分開討論,不能化簡為漂亮的公式。
二項式定理
(1-1)^0=C(0,0)*1^0*(-1)^0=1
為了避開這個問題,
所以限制二項式定理的次數為正整數,不可為0。
那麼巴斯卡三角形頂端的1又如何解釋?
定義0^0=1並不會有問題,而且在某些地方用得到。
反而不定義0^0=1根本就是給自己找麻煩。
迴響 由 Yee — 2011/05/19 @ 9:37 上午 |
我認為Taylor expansion 或多項式中的常數項寫成x^0只是為了方便用sigma 符號來書寫,並不涉及0^0的運算。
無可否認的是,實數系作為一個環,0^0=1是很方便而且很正常不過。
但實數系同時亦是一個域,因為域多了一個除法,這樣定義0^0為一個數己經有點奇怪:(0元)^(整數的0) = 1很合理,但(0元)^(0元)便講不通了(希望你明白我的意思)。更何況0亦是複數系中的一元,複數系中有對數及指數運算;0是對數的死敵,而在複數系中的指數運算是再複雜不過的。所以在複數系中的0^0是沒有意義的。
不過我認同(複數的0)^(整數的0)=1的講法。
迴響 由 Mark Shea — 2011/05/20 @ 3:38 上午 |
定義0^0=1
符合0^(-0)=1/0^0
這樣可以嗎?
在複數系中指數運算確實很複雜。
底數為0基本上比較不去討論,
而非不定義。
0^2=0
在複數系中又要如何討論?
總不會說0也不定義吧。
迴響 由 Yee — 2011/05/20 @ 7:33 上午 |
如果0^0要運算,
(0^0)^2=0^(0*2)
(0^2)^0=0^(2*0)
0^0*2^0=(0*2)^0
0^0/2^0=(0/2)^0
只要指數律中不遇到分母為0或0的負數次方,
都可以運算。
甚至
(0^0)^(-1)=0^[0*(-1)]
迴響 由 Yee — 2011/05/20 @ 7:37 上午 |
但你始終避免不了
ln (a^b) = b ln(a) 或 1/(a^b) = (1/a)^b
用在 0^0 的問題
尤其是 (0^0)^-1 (0^-1)^0
與其迴避所有用 1 是合法但以 0 為底數則不合法的運算,倒不如不去定義 0^0=1.
我認同只要指數律中不遇到分母為0或0的負數次方,0^0可以運算
所以 0^0 = 1 只適合於環(ring),但不適合於有除數(如域 field)或有對數的數系
複數系中的實數的實數次方的結果一定會和實數系的一樣,但 0^0 一樣是未下定義的
而 0^z = 0 若 z 0
迴響 由 Mark Shea — 2011/05/20 @ 10:29 上午 |
何以說避免不了?
(0^0)^-1 (0^-1)^0
遇到0的負數次方,不能這樣寫。
ln(0^0)=0*ln(0)
遇到底數為0,也不能這樣寫。
如果不願迴避,
則
0=0^1=0^(2-1)=0^2/0^1=0/0
ln(0^2)=2*ln(0)
是不是0也不要定義?
在複數系中,既然0的正數次方可以定義,
0的0次方也就一樣可以定義。
迴響 由 Yee — 2011/05/20 @ 10:41 上午 |
0=0^1=0^(2-1)=0^2/0^1=0/0
及
ln(0^2)=2*ln(0)
這正正是0不可做分母及ln(x)中x 的原因
所以1可以做分母及ln(x)中x
但0不可以
你不可用 1 用 0^0 代替
“在複數系中,既然0的正數次方可以定義,0的0次方也就一樣可以定義。"
完全沒有理據,邏輯完全錯誤
正如
“在複數系中,既然正數的逆可以定義,0的逆也就一樣可以定義。"
“在複數系中,既然正數的argument可以定義,0的argument也就一樣可以定義。"
迴響 由 Mark Shea — 2011/05/20 @ 11:01 上午 |
定義0^0=1,
並沒有讓0作分母及作ln(0),
找不出不定義的理由。
用1代替0^0,
找不出不可以的理由。
在複數系中不定義0^0=1的理由又是什麼?
要避免就避免,有什麼是避免不了的?
迴響 由 Yee — 2011/05/20 @ 12:14 下午 |
定義0^0=1
代表任何時候都可以用0^0代替1
無論是除數或對數或任何運算
如定義a^0=1當a0, 那任何時候都可以用a^0代替1,而不會出現問題
但0^0=1可以嗎?
那你認為在複數系中不定義0^0=1的理由又是什麼?
迴響 由 Mark Shea — 2011/05/20 @ 2:25 下午 |
任何時候,以1代替0^0都可以。
至於在複數系中不定義的理由,
我認為沒有。
迴響 由 Yee — 2011/05/20 @ 4:21 下午 |
任何時候,以0^0代替1都可以。
至於運算,會有限制,
代替了當然不代表可以無限制運算下去。
迴響 由 Yee — 2011/05/20 @ 4:24 下午 |
如果0^0代替1之後不可以無限制運算下去,那有什麼意思?
雖然不一定有需要用,但要確保可以用
所有定義一定要可以運算才有意義
迴響 由 Mark Shea — 2011/05/20 @ 5:41 下午 |
那請問複數系中定義 0^0 = 1 有什麼用呢?
迴響 由 Mark Shea — 2011/05/20 @ 5:54 下午 |
牽扯到0的運算,
本來就有許多限制。
不管定不定義0^0=1都會如此。
至於要運算,
我已經舉例0^0=1可以做某些運算了。
並非完全不能做運算。
反而不定義,
遇到可以用時還不敢用,
卻要東閃西躲、徒增困擾。
泰勒展開式為何要把常數項分開寫,不直接用Σ化簡?
二項式定理為何次數必須為正整數,而不是非負整數?
如此一來要如何解釋巴斯卡三角形頂端的1?
迴響 由 Yee — 2011/05/20 @ 6:00 下午 |
請問複數系中定義0的正數次方為0又有什麼用?
迴響 由 Yee — 2011/05/20 @ 6:01 下午 |
這些是比較具體的理由,
還有一些抽象的觀念,也支持0^0=1。
一、在組合數學中,
n!是n物作直線排列的方法數,
C(m,n)是從m物取n物的方法數,
m^n是將n物分配給m人的方法數。
0!=1
C(0,0)=1
意即:
0物作直線排列的方法數是1,
從0物取0物的方法數是1,
同樣的,將0物分配給0人的方法數也是1。
那就是0^0=1。
二、
請問0個數的和是多少?
再來,請問0個數的乘積是多少?
迴響 由 Yee — 2011/05/20 @ 6:15 下午 |
請問複數系中定義0的正數次方為0又有什麼用?
複數系中定義1的正數次方又有什麼用?
複數系中定義2的正數次方又有什麼用?
我想答案是一樣的
迴響 由 Mark Shea — 2011/05/20 @ 11:18 下午 |
同樣的,將0物分配給0人的方法數也是1
=> 那就是0^0=1
???
我對這點有存疑, 因為
m物分配給n人的方法數
是 m/n , 對嗎?
迴響 由 Mark Shea — 2011/05/20 @ 11:19 下午 |
假若0^0是存在的話,一定只是滿足非負指數的指數律
因為0的負數次方不存在,所以不滿足負指數的指數律
0^0的運算要排除在分母以外,所以0^0不適用於有除法運算的集合
迴響 由 Mark Shea — 2011/05/21 @ 2:11 上午 |
1.
還有冪級數, 多項式, 二項式定理都只涉及乘數,皆沒有除數
2.
而實數 R 上的冪級數或多項式可以看成 R[[x]] (formal power series) 及 R[x] (polynomial)
即多項式可以看成實數 R 的一個序列,subsitition 即是 R[x] 到 R 上的一個 homomorphism
而這個 homomorphism 的結果和多項式作為函數的結果完全一模一樣
即是說,不需要計算0^0也可以計算 P(0)
3.
而所有所謂可以"證明" 0^0=1的事實包括
0物取0物的取法, 空集至空集的映射數目等都是廢話,都是為了迎合0^0=1而定義的
試想想:0物取1物的取法 = 0 可以理解,但0物取0物的取法 = 1 便不可理解
還有空集至空集的映射數目 = 1 但空集至整數集的映射 = 空集,更加不可理喻
怎可以作證明呢!
4.
巴斯卡三角形頂端的1不是因為(1+x)^0 = 1 嗎? (x不等於-1)
這裏我們不能因為(1+x)^n對所有 x 都有定義就說(1+x)^0對於所有實數 x 都有定義!
這是犯嚴重錯誤的歸納法。
至於展開後的式子中的 x^0 可以參考本貼第二點
5.
分析學中x^y在(0,0)並不連續,x^y應該是undefined 或 indeterminate
6.
正如 Donald C. Benson 所言:
The choice whether to define 0^0 is based on convenience, not on correctness
定義 0^0=1 只是方便書寫及記憶,但你不能證明它或證明它不是undefined
至少 ring 上的 0^0=1 是合理,但 field 上的 0^0=1 便會帶來不方便!
迴響 由 Mark Shea — 2011/05/21 @ 2:54 上午 |
將n物分配給m人的方法數是m^n。
平均每個人拿到的個數是n/m。
迴響 由 Yee — 2011/05/21 @ 5:32 上午 |
在複數系中定義0^0=1有什麼用?
你希望得到什麼答案?
有什麼理由在某些領域定義,某些領域不定義?
這樣反而徒增困擾。
除非你找到定義會產生的問題。
迴響 由 Yee — 2011/05/21 @ 5:42 上午 |
0^0的運算要排除在分母以外,
所以0^0不適用於有除法運算的集合。
0本身也是一樣。
迴響 由 Yee — 2011/05/21 @ 5:44 上午 |
0物取0物的方法數,
我已經說過這是抽象的觀念。
而且這本來就不是證明。
定義不就證明。
迴響 由 Yee — 2011/05/21 @ 5:46 上午 |
“巴斯卡三角形頂端的1不是因為(1+x)^0 = 1 嗎? (x不等於-1)"
為何要限制x不等於-1?
多加限制不是產生更多不便嗎?
而且這種限制是為了迎合不定義0^0=1。
定義0^0=1就不用限制了。
迴響 由 Yee — 2011/05/21 @ 5:49 上午 |
不連續仍然可以定義。
只是在不連續點上定義函數值。
並沒有什麼不妥。
定義不用證明。
定義的理由是有用處。
迴響 由 Yee — 2011/05/21 @ 5:52 上午 |
不是因為(1+x)^n對所有x都有定義
就說(1+x)^0對於所有實數x都有定義!
而是定義0^0=1,
可以讓(1+x)^0對於所有實數x都有定義。
這樣式子就會很漂亮。
迴響 由 Yee — 2011/05/21 @ 6:06 上午 |
請問0個數的和是多少?
0個數的乘積是多少?
迴響 由 Yee — 2011/05/21 @ 6:08 上午 |
0 要排除在除法以外,因為這是域
1=0^0 如果排除在除法以外,請問這是什麼代數結構?
迴響 由 Mark Shea — 2011/05/21 @ 7:46 上午 |
(0^0)^(-1)=0^(-0)=1/0^0
可以作除法運算,並沒有排除在外。
迴響 由 Yee — 2011/05/21 @ 10:48 上午 |
1/(0^0) = (1/0)^0 ?+
迴響 由 Mark Shea — 2011/05/22 @ 7:57 上午 |
0可以排除在除法之外,
這個式子不成立。
更何況,你是根據什麼寫出這個式子?
指數律。
指數律可以這樣用嗎?
迴響 由 Yee — 2011/05/22 @ 8:44 上午 |
所以我咪話指數律唔可以咁用
係因為你有個 0 做底數
迴響 由 Mark Shea — 2011/05/24 @ 9:57 下午 |
我一直強調 0^0=1 係可以方便書寫及運算
同時亦限制了一些運算,因為 0 不可以做底數
使得 (a^b)^-1 != (a^-1)^b
迴響 由 Mark Shea — 2011/05/24 @ 10:01 下午 |
所以0^0應該定義為1。
而且在運算上有一些限制。
迴響 由 Yee — 2011/05/24 @ 10:09 下午 |
所謂的“應該定義"是根據合理性。
以目前找到的理由來看,
不定義為1很不應該。
迴響 由 Yee — 2011/05/25 @ 7:21 上午 |
0是加法的恆等元素(identity element),
所以0個數的總和等於0。
同樣的,1是乘法的恆等元素,
所以0個數的乘積等於1。
這不僅可以解釋0^0=1,也可以解釋0!=1。
迴響 由 Yee — 2011/05/25 @ 9:42 上午 |
0個數的乘積等於1,
是一個有點抽象的觀念。
這可不是僅僅為了方便書寫而已。
迴響 由 Yee — 2011/05/25 @ 12:15 下午 |
把連續性視為無限上綱,
不定義不連續點的函數值。
以致要使用到0^0=1時又不敢用,
而要東閃西躲,徒增困擾。
這是目前數學界不願面對的問題。
迴響 由 Yee — 2011/05/26 @ 9:14 上午 |
其實想問,目前世界數學界面對的最大問題是甚麼?(Well, this is not a well-defined question, may be…)單談香港數學教育界,面對的問題也不少。
迴響 由 johnmayhk — 2011/05/26 @ 9:25 上午 |
我無法回答最大的問題是什麼。
但0^0的問題確實存在,
而且定義為1就可以輕易解決了。
迴響 由 Yee — 2011/05/26 @ 9:58 上午
二項式定理:
在定義0^0=1的前提下,
(x+y)^n
=ΣC(n,k)x^k*y^(n-k){k=0到n}
x,y為複數,n為非負整數。
公式寫得乾淨俐落。
在不定義0^0=1的前提下,
n只能為正整數,
公式要如何寫才正確?
多項式:
對於項次為n+1項之多項式,
c[0]+c[1]*x^1+c[2]*x^2+…+c[n]*x^n
n為非負整數。
在定義0^0=1的前提下,
上式=Σc[k]*x^k{k=0到n}
在不定義0^0=1的前提下,
公式要如何寫才正確?
迴響 由 Yee — 2011/11/30 @ 12:41 下午 |
沒有限制x,y不可為0,
如果不定義0^0=1,
公式中就必須避開所有0次方的可能。
迴響 由 Yee — 2011/12/01 @ 7:00 下午 |
迴響 由 haha — 2011/12/03 @ 9:04 下午 |
一、
1*0=0
1可以為任意數,
所以1無法定義?
二、
0^x=0僅對x>0成立,
對x<0不成立。
推論0^0可能為0很牽強。
至於x^0=1,
只要定義0^0=1,
就沒有例外,
合理性很強。
不過即使極限不存在,
函數值仍然可以定義。
沒有理由把極限無限上綱化。
迴響 由 Yee — 2011/12/04 @ 2:20 下午 |
(0^0)^2=0^(0*2)=0^0
0^(-0)=1/0^0
0^0=1是唯一合理的結果。
迴響 由 Yee — 2011/12/04 @ 2:30 下午 |
定義 0^0 = 1 並沒有太大的問題。如果不定義,到了方陣的 0 次方會很難搞,冪零方陣的 0 次方應該是單位方陣的。
數學本來就是建立在無須定義的公理上(集合論、一階邏輯)。當我們不斷要求證明時,總要停止在無需證明的公理上,否則只會形成無窮迴圈。
用 0^0 = 0/0 說它無法定義是很荒謬的。如果這樣不荒謬,那我也可以說 0^2 = (0^1)^3 / 0^1 之類的讓 0 的正數次方也死掉。
任何數的 0 次方都應該是 1。(任何數乘以 0 都應該是 0)
任何方陣的 0 次方都應該是單位方陣。(任何矩陣乘以零矩陣都應該是零矩陣)
「沒有東西」取 product 的結果,一定是乘法單位元。(「沒有東西」取 sum 的結果,一定是加法單位元)
迴響 由 Chen-Pang He — 2012/06/26 @ 5:03 下午 |
Thanks!
But what do you think about the comment #91 of the following post:
迴響 由 johnmayhk — 2012/06/26 @ 10:12 下午 |
方陣難搞的地方,
在純量中一樣難搞。
只有定義0^0=1才能解決。
迴響 由 Yee — 2012/07/06 @ 10:27 下午 |
-1^0=?
迴響 由 22257412 — 2012/07/25 @ 10:19 上午 |
-1^0=-(1^0)=-1
迴響 由 johnmayhk — 2012/07/25 @ 11:47 上午 |